ハウスドルフ次元

ハウスドルフ次元（ハウスドルフじげん、英: Hausdorff dimension）は、フェリックス・ハウスドルフが導入した非負実数値の次元である。フラクタルのような複雑な図形ないし集合の次元を表す道具として用いられる。ハウスドルフ測度を使って定義される次元で、ある集合のハウスドルフ次元は、その集合のハウスドルフ測度が ∞ から 0 へ移る不連続点から定義される。

ハウスドルフの後に、アブラム・ベシコビッチが研究を深めて更に明確化した。そのため、ハウスドルフ・ベシコビッチ次元（ハウスドルフ・ベシコビッチじげん、英: Hausdorff-Besicovitch dimension）とも呼ばれる。フラクタル幾何学や実解析で重要な役割を果たし、特にフラクタル幾何学では最重要概念の一つである。一般的に与えられた集合のハウスドルフ次元を決定するのは困難であるが、自己相似集合などの一部のクラスの集合では求め方が確立している。確定的な定義ではないが、ハウスドルフ次元が位相次元より大きな集合がフラクタルと定義づけられる。

背景

一般的な「次元」という言葉は、現実世界の空間が高さ・幅・奥行きの3つから成るので3次元と呼ぶ考え方に立脚している。この考え方の延長上で、平面は縦・横から成るので2次元で、直線や線分は1次元であるという風に考えられてきた。数学の世界でも、19世紀終わり近くまで、点が 0 次元、直線が 1 次元、平面が 2 次元、…という素朴な次元の概念しか存在しなかった。しかし、19世紀後半に、ゲオルク・カントールが平面上の点と直線上の点が1対1対応を持つことを、ジュゼッペ・ペアノが単位区間から正方形の上への連続写像を構成できることを発見し、数学界で次元の概念の再考が迫られた。その後、位相不変で整数値を取る位相次元（正確には被覆次元、大きな帰納的次元、小さな帰納的次元がある）が、次元の精密な定義として導入された。

一方、「長さ」「面積」「体積」といった直感的概念についても一般の集合に拡張させる動きが、19世紀末から20世紀初頭にかけてエミール・ボレルやアンリ・ルベーグによって進められた。1914年、コンスタンティン・カラテオドリは n 次元ユークリッド空間内の s 次元測度を定義した。カラテオドリの定義では s は整数値であった。1919年、カラテオドリの仕事を引き継いだフェリックス・ハウスドルフは、カラテオドリの定義は非整数の s に対しても意味があることを指摘し、後にハウスドルフ次元（英: Hausdorff dimension）と呼ばれる非整数次元を導入した。ハウスドルフは、カントールの3進集合のハウスドルフ次元が log 2/log 3 = 0.6309… であることを実際に示してみせた。

ハウスドルフの後に、ハウスドルフ次元およびハウスドルフ測度の概念を明確化を担ったのはアブラム・ベシコビッチである。そのため、彼の名も取ってハウスドルフ次元はハウスドルフ・ベシコビッチ次元（英: Hausdorff-Besicovitch dimension）とも呼ばれる。ハウスドルフ測度とそれを使った幾何学の数学的成果の多くはベシコビッチによって与えられた。ブノワ・マンデルブロは「ハウスドルフが標準的でない次元の父であったのに対し、ベシコビッチは、その母であった」と評している。

そのマンデルブロは、自然の海岸線や樹木の形の数学的理想化として、カントールの3進集合やコッホ曲線やワイエルシュトラス関数などの以前より報告されていた特異な数学的集合の総称として、フラクタルという概念と名称を与えた。マンデルブロは、1977年のエッセイ「Fractals: Form, Chance and Dimension」で、ハウスドルフ次元が位相次元よりも大きい集合をフラクタルの数学的な定義とした。1982年の著書「The Fractal Geometry of Nature」でフラクタルの概念は一躍有名となり、フラクタルは各分野で研究され始めた。次元はフラクタル幾何学の中心的概念であり、その中でも最重要なのがハウスドルフ次元である。ハウスドルフ測度およびハウスドルフ次元はフラクタル幾何学や実解析で重要な役割を果たす。

定義

ハウスドルフ測度

次元を定義したい図形として、n-次元ユークリッド空間 ℝⁿ 上の空ではない部分集合 X を考える。ユークリッド空間に限定せずに、一般の距離空間でもよい。X 上の 2 点 x, y のユークリッド距離を d(x, y) で表す。集合 X の直径を次で定義する。

${\displaystyle \left\vert X\right\vert =\sup\{d(x,y)\ |\ x,y\in X\}}$

ここで sup は上限を意味し、d(x, y) は x と y のユークリッド距離である。単純に言えば、直径とは集合 X の中のもっとも離れた2点間の距離を意味している。

ある X が与えられたとき、それに対する可算個の集合族 {U_i} による被覆を考える。ただし、{U_i} それぞれの直径は、ある正の実数 δ 以下とする。このような {U_i} を δ 被覆と呼ぶ。すなわち、

${\displaystyle X\subset \bigcup _{i=1}^{\infty }U_{i}}$ かつ ${\displaystyle \left\vert U_{i}\right\vert \leq \delta }$

である。{U_i} は有限個でもよい。

さらに、各々の U_i の直径を正の実数 s で冪乗したものの総和 ∑∞
i = 1|U_i|^s を取る。そして、δ と s の値を固定し、X に対して可能なあらゆる δ 被覆 {U_i} を考えた場合の ∑∞
i = 1|U_i|^s の下限を取る。これを

${\displaystyle H_{\delta }^{s}(X)=\inf \sum _{i=1}^{\infty }\left\vert U_{i}\right\vert ^{s}}$

と定義する。

被覆を抑える2つの直径 δ が δ₂ < δ₁ という大小関係にあるとする。このとき、直径を δ₁ 以下とする被覆は、直径を δ₂ 以下とする被覆を含んでいる。よって、H s
δ₁ の値は、H s
δ₂ よりも小さいか等しいかのいずれかとなる。結局、

${\displaystyle \delta _{2}<\delta _{1}}$ ならば ${\displaystyle H_{\delta _{2}}^{s}(X)\geq H_{\delta _{1}}^{s}(X)}$

であるから、H s
δ は δ の減少とともに単調増加する。したがって、

${\displaystyle H^{s}(X)=\lim _{\delta \to 0}\inf \sum _{i=1}^{\infty }\left\vert U_{i}\right\vert ^{s}}$

という極限値が、 H ^s(X) = ∞ の場合まで含めると常に存在する。この H ^s(X) は外測度の条件を満たし、s 次元ハウスドルフ外測度やハウスドルフ s 次元外測度と呼ばれる。さらに、可測集合（または σ-集合体）に制限した H ^s は s 次元ハウスドルフ測度やハウスドルフ s 次元測度と呼ばれる。

ハウスドルフ次元

上記のように定義された s 次元ハウスドルフ外測度 H ^s(X) を、X を固定して s の関数として見る。s < t を満たす任意の s と t について、δ 被覆は、

${\displaystyle \sum _{i=1}^{\infty }\left\vert U_{i}\right\vert ^{t}=\sum _{i=1}^{\infty }\left\vert U_{i}\right\vert ^{t-s}\left\vert U_{i}\right\vert ^{s}\leq \delta ^{t-s}\sum _{i=1}^{\infty }\left\vert U_{i}\right\vert ^{s}}$

を満たすので、

${\displaystyle H_{\delta }^{t}(X)\leq \delta ^{t-s}H_{\delta }^{s}(X)}$

という関係が成り立つ。よって、δ → 0 である H ^s(X) は s の単調減少関数である。

さらに、上の関係により、H ^s(X) < ∞ であるならば H ^t(X) = 0 である。また、H ^t(X) > 0 であるならば、H ^s(X) = ∞ である。したがって、H ^s(X) を s の関数として見たとき、H ^s(X) は高々 1 つの第一種不連続点 s を持つ。この不連続点を D と表すと、

${\displaystyle {\begin{aligned}D&=\inf\{s\in [0,\ \infty )|H^{s}(X)=0\}\\&=\sup\{s\in [0,\ \infty )|H^{s}(X)=\infty \}\end{aligned}}}$

を満たす D ≥ 0 が唯一定まる。ハウスドルフ次元またはハウスドルフ・ベシコビッチ次元とは不連続点 D の値のことで、これを dim_H(X) や dim_H X などと表して

${\displaystyle \dim _{H}(X)=\inf\{s\in [0,\ \infty )|H^{s}(X)=0\}}$

あるいは、

${\displaystyle \dim _{H}(X)=\sup\{s\in [0,\ \infty )|H^{s}(X)=\infty \}}$

で定義される。

直感的説明

ハウスドルフ次元の意味を直感的に説明すると、ハウスドルフ外測度 H ^s(X) の次元 s はものさしの粗さのようなもので、s < dim_H(X) で H ^s(X) = ∞ となるのは、集合 X の厚さを測るのには s がものさしとして細か過ぎて、そのものさしからは X は捕え切れないほど大きく見える状態である。一方、s > dim_H(X) で H ^s(X) = 0 となるのは、集合 X の厚さを測るのには s がものさしとして粗過ぎて、そのものさしからはX の厚さは無視できるほど小さく見える状態である。s = dim_H(X) は、それらの中間で、X の厚さを測るのにちょうどいい粗さのものさしであることを意味している。

ハウスドルフ外測度を定義するために出てきた ∑∞
i = 1|U_i|^s という和は、s = 1 を代入してみると、∑∞
i = 1|U_i|¹ という長さ |U_i| の線分の長さの合計となる。これを使って集合 X のハウスドルフ外測度を求めるという行為は、X の長さのような量を決めているのに等しい。集合 X が曲線だとすれば、X は実際に長さに相当する量を持っているので、s = 1 のハウスドルフ外測度でその長さを測ることができる。同様に s = 2 で考えると、∑∞
i = 1|U_i|² は一辺長さが |U_i| の正方形の面積の合計である。よって、集合 X が面であれば、s = 2 で適切にその面積を測ることができる。

このように、ある集合の長さや面積のような量を測るにあたっては、適切な s の値が存在する。適切な s の値は、逆にその集合を特徴づけすることができる値とも捉えられる。曲線ならば s = 1 で面ならば s = 2 であったが、集合がもっと複雑になれば自然数ではない s の値が最適ということもありうる。このような考え方にもとづいて、 ∑∞
i = 1|U_i|^s 自体の値ではなく、s の方の最適値に着目して定義としたのがハウスドルフ次元といえる。

基本的性質

ハウスドルフ次元は、「次元」と呼ばれるものが当然満たすであろう次の基本的な性質を満たす。

• A ⊂ B ⊂ ℝⁿ であれば、dim_H(A) ≤ dim_H(B) である
• A ⊂ ℝⁿ が開集合であれば、常に dim_H(A) = n である
• A₁, A₂, A₃, … を可算個の集合列とすると、dim_H(∪_i A_i) = sup{dim_H(A_i)} である
• A が可算集合であれば、常に dim_H(A) = 0 である
• A が ℝⁿ 上の滑らかな m 次元多様体であれば、dim_H(A) = m である

また、A ⊂ ℝⁿ に対して、s > n ならば H^s(A) = 0 なので、常に dim_H(A) ≤ n である。

位相次元は同相写像に対して不変であることが一般的だが、ハウスドルフ次元はこの性質は持たない。しかし、写像 f : X → ℝⁿ がリプシッツ連続であれば、すなわち、ある正の定数 c が存在して任意の x, y ∈ X ⊂ ℝⁿ に対して

${\displaystyle d(f(x),\ f(y))\leq cd(x,\ y)}$

を満たすならば

${\displaystyle \dim _{H}(f(X))\leq \dim _{H}(X)}$

が成り立つ。さらに f が双リプシッツであれば、すなわち、ある正の定数 c₁ と c₂ が存在して任意の x, y ∈ X に対して

${\displaystyle c_{1}d(x,\ y)\leq d(f(x),\ f(y))\leq c_{2}d(x,\ y)}$

を満たすならば

${\displaystyle \dim _{H}(f(X))=\dim _{H}(X)}$

が成り立つ。これによって、位相幾何学で同相写像の存在によって2つの集合を「同じ」と見なすように、フラクタル幾何学では双リプシッツ写像の存在によって「同じ」と見なす取り組み方が成立する。

ℝⁿ の部分集合を Aとし、ℝ^m の部分集合を Bとすると、これらの直積集合 A × B = {(x, y) ∈ ℝ^{n m}  |  x ∈ ℝⁿ, y ∈ ℝ^m} のハウスドルフ次元について一般的に成り立つ関係は

${\displaystyle \dim _{H}(A\times B)\leq \dim _{H}(A) \dim _{H}(B)}$

である。しかし、後述の dim_B に対して dim_H(X) = dim_B(X) が満たされるならば、

${\displaystyle \dim _{H}(A\times B)=\dim _{H}(A) \dim _{H}(B)}$

が成り立つ。

射影に関しては、X を ℝⁿ の部分空間へ写す正射影を p(X) とすると

${\displaystyle \dim _{H}(p(X))\leq \dim _{H}(X)}$

が一般的な関係として成り立つ。

計算

定義からの直接計算

一般的に、与えられた集合 X のハウスドルフ次元を決定するのは困難である。次元を決定するためによく使われる手法は、上からの評価と下からの評価を行い、それらが同じ値を取ることを証明する手法である。すなわち、dim_H(X) ≤ s（上から）かつ dim_H(X) ≥ s（下から）であることを証明すれば dim_H(X) = s である。上からの評価は比較的簡単で、特殊な δ 被覆を設定すれば求まる。特に一般的に大変なのが、ハウスドルフ測度およびハウスドルフ次元の下からの評価を得ることである。下からの評価のためにはあらゆる被覆を考えて決める必要があり、難しくなる。

数直線 ℝ¹ 上の図形であれば、定義からの直接計算でもハウスドルフ次元の決定は比較的容易である。ハウスドルフ次元が非整数を取る図形の中でもっとも有名な集合として、カントール集合がある。カントール集合ないしカントールの3進集合とは、線分 1 の中央から1/3の長さの線分を除去し、さらに残った2つの線分の中央のそれぞれの1/3の長さの線分を除去し、という操作を繰り返し無限回行うことで得られる図形である。カントール集合を作る途中の k 番目の操作でできる図形を C_k と表すと

${\displaystyle C_{k}=\left[0,{\frac {1}{3^{k}}}\right]\cup \left[{\frac {2}{3^{k}}},{\frac {3}{3^{k}}}\right]\cup \ldots \cup \left[{\frac {3^{k}-1}{3^{k}}},1\right]}$

であり、カントール集合を C と表すと

${\displaystyle C=\bigcap _{k=1}^{\infty }C_{k}}$

と定義される。カントール集合はハウスドルフ次元を正確に決定できる少ない例のうちの一つである。

カントール集合のハウスドルフ測度およびハウスドルフ次元の場合、I_k を C に対する δ 被覆と考えれば、上からの評価が得られる。この被覆について s = log 2/log 3 と仮定すると、 H ^s(C) ≤ 1 および dim_H(C) ≤ s であることが得られる。また、少し技巧的な証明を要するが、任意の閉区間による被覆に対して H ^s(C) ≥ 1 および dim_H(C) ≥ s であることが得られる。したがって、dim_H(C) = log 2/log 3 である。

自己相似集合の場合

フラクタルの中でも、ハウスドルフ次元を正確かつ簡単に決定できるクラスの集合がある。写像 f : ℝⁿ → ℝⁿ が、ある定数 c_i < 1 が存在して、

${\displaystyle \left\vert f(x)-f(y)\right\vert \leq c_{i}\left\vert x-y\right\vert }$

が任意の x, y ∈ ℝⁿ について成り立つとき、f を縮小写像という。m ≥ 2 個の縮小写像の組 f₁, f₂, …, f_m : ℝⁿ → ℝⁿ が与えられたとき、

${\displaystyle U\bigcup _{i=1}^{m}f_{i}}$

を満たすコンパクト集合 U ⊂ ℝⁿ を自己相似集合という。自己相似集合 U が

${\displaystyle \bigcup _{i=1}^{m}f_{i}\subset U}$

かつ任意の i と j ≠ i について

${\displaystyle f_{i}(U)\cap f_{j}(U)=\emptyset }$

を満たすとき、U は開集合条件を満たすという。

さらに、m ≤ 2 個の縮小写像の組における各写像 f_i について、ある定数 c_i < 1 が存在し、

${\displaystyle \left\vert f_{i}(x)-f_{i}(y)\right\vert =c_{i}\left\vert x-y\right\vert }$

が任意の x, y ∈ ℝⁿ について成り立つとき、f_i は相似縮小変換などと呼ばれる。定数 c は縮小率と呼ばれる。すなわち、f_i は縮小、回転、平衡移動、反転などの変換を組み合わせて、ℝⁿ 上の部分集合を幾何学的に相似な集合に写す線形変換である。

以上のように、縮小写像が相似縮小変換でなおかつ開集合条件を満たすとき、その縮小写像の組から定まる自己相似集合 U のハウスドルフ次元は

${\displaystyle \sum _{i=1}^{m}(c_{i})^{s}=1}$

を満たす s と等しいことが定理として成り立つ。この定理より、多くの自己相似フラクタルのハウスドルフ次元が求まる。カントールの3進集合は m = 2, c₁ = 1/3, c₂ = 1/3 という開集合条件を満たす相似縮小変換で構成できるため、上記の定理からハウスドルフ次元 log 2/log 3 を求めることもできる。

例

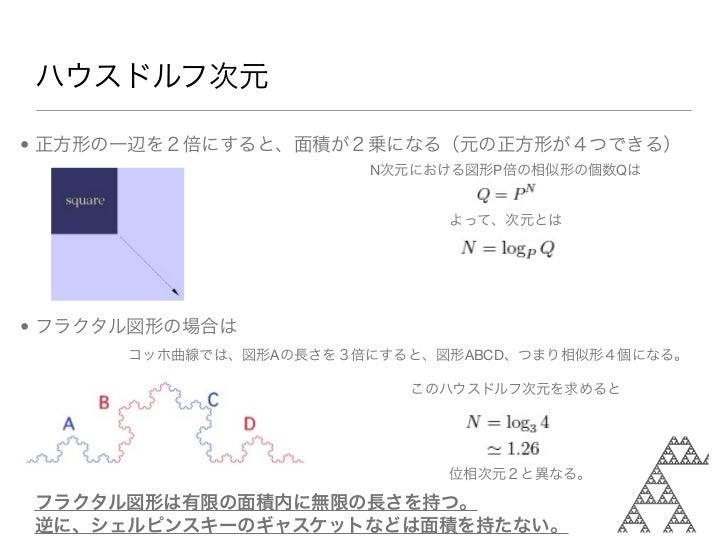
カントールの3進集合のハウスドルフ次元は log 2/log 3 = 0.6309… であったが、一般化したカントール集合、例えば線分の真ん中を 1 − 2k 除去する場合は、ハウスドルフ次元は log 2/log 1/k である。カントール集合と同様に再帰的な手続きから構成できるフラクタル図形の単純な例には、コッホ曲線 K、シェルピンスキー・ガスケット S などがある。これらも開集合条件を満たす相似縮小変換であり、それぞれのハウスドルフ次元は dim_H(K) = log 4/log 3 = 1.2618… と dim_H(S) = log 3/log 2 = 1.5849… である。

力学系でもフラクタルが様々な形で現れる。α 倍に縮む散逸系のパイこね変換のアトラクターはハウスドルフ次元 1 log 2/−log α である。複素力学系のマンデルブロ集合は非常な複雑な図形だが連結で、その境界はハウスドルフ次元 2 である。

規則的に作られる自己相似フラクタルの外に、自然界で見られるようなランダムパターンから生まれる自己相似フラクタルもある。ℝⁿ 上のブラウン運動の軌跡は、n ≥ 2 であれば n の値にかかわらず確率 1 でハウスドルフ次元 2 である。

ハウスドルフ次元が位相次元よりも大であることをフラクタルの定義とすると、直感的にはフラクタルに相応しいような図形がフラクタルにならない例もある。例えば、カントールの悪魔の階段や高木関数のグラフは、位相次元・ハウスドルフ次元ともに 1 である。連続曲線でありながら平面を充填するペアノ曲線も、位相次元・ハウスドルフ次元ともに 2 で一致する。こういった集合の存在が、フラクタルの定義に改善の余地がある理由の一つである。

ハウスドルフ次元の決定が数学上の未解決問題となっているものには、次のようなものがある。ℝⁿ 上の部分集合 K が有界閉で、全ての方向の長さ 1 の線分を含み、さらに n 次元ルベーグ測度が 0 のとき、K を n 次元掛谷集合と呼ぶ。n 次元掛谷集合のハウスドルフ次元は n であろうと予想されており、掛谷予想や掛谷問題と呼ばれる。2 次元掛谷集合のハウスドルフ次元は 2 であることは証明されたが、3 次元以上は未解決である。

他の次元との関係

位相次元

縦・横・高さという直感的な次元は位相次元と呼ばれる。上で述べたように、A が ℝⁿ 上の滑らかな m 次元多様体であれば、dim_H(A) = m であるので、ハウスドルフ次元は位相次元と矛盾しない拡張となっている。位相次元と呼ばれるものは正確には被覆次元、大きな帰納的次元、小さな帰納的次元の3つがあるが、ユークリッド空間上では3者は常に一致する。以下、 ℝⁿ 上の集合 X の位相次元を dim_T(X) と表す。

位相次元 dim_T(X) とハウスドルフ次元 dim_H(X) は一致することもあれば、異なることもある。例えば、線分の dim_T(X) と dim_H(X) は共に 1 で、正方形の dim_T(X) と dim_H(X) は共に 2 である。このような単純な図形では dim_T(X) と dim_H(X) は一致するが、図形が複雑になると相異なってくる。しかし一般的な関係として、任意の集合 X の位相次元とハウスドルフ次元は

${\displaystyle \dim _{T}(X)\leq \dim _{H}(X)}$

という関係が成り立つ。例えば、カントールの3進集合 C は dim_H(C) = log 2/log 3 = 0.6309… だが、dim_T(C) = 0 である。

フラクタルの提唱者であるブノワ・マンデルブロ自身のフラクタルの定義は、ハウスドルフ次元が位相次元よりも高い集合（図形）がフラクタルとされる。ただし、マンデルブロも述べているように、このフラクタルの定義は確定的ではない。「フラクタル次元」という言葉はしばしば曖昧に用いられ、定義が与えられずに用いられたり、使う人によっては定義が異なったりするが、一つの考え方としては非整数値を取る次元をフラクタル次元と呼ぶ。マンデルブロはハウスドルフ次元のことをフラクタル次元と言い換えており、文献によってはフラクタル次元とはハウスドルフ次元を指す。

ボックス次元

ハウスドルフ次元は数値の具体的な計算が難しいという欠点がある。これに対し、被覆する集合の直径を全て同じとしたのがボックス次元と呼ばれる次元で、ハウスドルフ次元よりも数学的には扱いにくいが計算は容易である。ボックス次元には同値な定義がいくつかあるが、集合 X に対して

${\displaystyle {\underline {\dim }}_{B}(X)=\lim _{\epsilon \rightarrow 0}\inf {\dfrac {\log N_{\delta }(X)}{\log {\frac {1}{\delta }}}}}$

${\displaystyle {\overline {\dim }}_{B}(X)=\lim _{\epsilon \rightarrow 0}\sup {\dfrac {\log N_{\delta }(X)}{\log {\frac {1}{\delta }}}}}$

とおいて、

${\displaystyle {\underline {\dim }}_{B}(X)={\overline {\dim }}_{B}(X)={\dim }_{B}(X)}$

が成り立つとき、dim_B(X) を X のボックス次元という。ここで、δ は X を被覆する開被覆の直径、N_δ(X) は X を被覆するのに必要な δ 開被覆の最小個数を表す。ハウスドルフ次元とボックス次元には、一般的に

${\displaystyle \dim _{H}(X)\leq {\underline {\dim }}_{B}(X)\leq {\overline {\dim }}_{B}(X)}$

あるいは

${\displaystyle \dim _{H}(X)\leq \dim _{B}(X)}$

という関係が成り立つ。

相似次元

上記の#自己相似集合の場合に求められる次元 s は、相似次元とも呼ばれる。相似次元は自己相似性の観点から得られる。例えば、ある線分を 1/3 倍したコピーを考えると、元の線分はそのコピー 3 = 3¹ 個から成り立っている。また、ある正方形を 1/3 倍したコピーを考えると、元の正方形はそのコピー 9 = 3² 個から成り立っている。そして、ある立方体を 1/3 倍したコピーを考えると、元の立方体はそのコピー 27 = 3³ 個から成り立っている。線分、正方形、立方体のそれぞれの次元 1, 2, 3 は、コピーの個数の指数として現れている。これを一般化すると、c 倍したコピーを考えると元の図形はそのコピーの m 個から成り立つとき、次元 s と c と m のあいだには

${\displaystyle N=\left({\frac {1}{c}}\right)^{s}}$

という関係がある。よって次元 s は

${\displaystyle s={\frac {\log N}{\log(1/c)}}}$

と定義でき、これを相似次元と呼ぶ。

一般的な相似次元は、縮小写像の m 個の組 f₁, f₂, …, f_m : ℝⁿ → ℝⁿ が与えられたときに、これに対応する自己相似集合に対して、それぞれの縮小率 c_i (i = 1, 2, … m) から

${\displaystyle \sum _{i=1}^{m}(c_{i})^{s}=1}$

を満たす s の正の値によって与えられる。自己相似集合を X として、その相似次元を dim_S(X) と表すとする。上記のとおり、縮小写像が相似縮小変換でなおかつ開集合条件を満たすとき、その自己相似集合のハウスドルフ次元と相似次元には

${\displaystyle \dim _{H}(X)=\dim _{S}(X)}$

という関係がある。また、相似縮小変換かつ開集合条件という条件を付与しない一般的な自己相似集合については、ハウスドルフ次元と相似次元の関係は次のようになる。

${\displaystyle \dim _{H}(X)\leq \dim _{S}(X)}$

出典

参照文献

• Kenneth Falconer、服部 久美子・村井 浄信（訳）、2006、『フラクタル幾何学』、共立出版〈新しい解析学の流れ〉 ISBN 4-320-01801-X
• K.J.ファルコナー、畑 政義（訳）、1989、『フラクタル集合の幾何学』初版、近代科学社 ISBN 4-7649-1013-6
• 山口 昌哉・畑 政義・木上 淳、1993、『フラクタルの数理』初版、岩波書店〈岩波講座 応用数学1 [対象7]〉 ISBN 4-00-010511-6
• 本田 勝也、2002、『フラクタル』初版、朝倉書店〈シリーズ非線形科学入門1〉 ISBN 978-4-254-11611-3
• 石村 貞夫・石村 園子、1990、『フラクタル数学』初版、東京図書 ISBN 4-489-00332-3
• 青木 統夫、2004、『測度・エントロピー・フラクタル』初版、共立出版〈非線形解析III〉 ISBN 4-320-01773-0
• 山口 昌哉、1986、『カオスとフラクタル ―非線形の不思議―』、講談社〈ブルーバックス B-652〉 ISBN 4-06-132652-X
• B.マンデルブロ、広中 平祐（監訳）、2011、『フラクタル幾何学　下』、筑摩書房〈ちくま学芸文庫〉 ISBN 978-4-480-09357-8
• 新井 仁之、2023、『ルベーグ積分講義 ―ルベーグ積分と面積0の不思議な図形たち―』改訂版、日本評論社 ISBN 978-4-535-78945-6

外部リンク

• Hausdorff dimension - Encyclopedia of Mathematics
• Hausdorff Dimension - MathWorld
• 掛谷予想とハウスドルフ次元：掛谷問題入門 No.3 - YouTube
• Hausdorff次元 - J-GLOBAL